(This essay used to be on a different month, but I rearranged things so now it's here for May!)
I decided to talk about the roots of functions and give motivation to why we care about finding these things. In the last month of teaching Intermediate Algebra, I wanted to give motivation why we were looking at different methods to factor quadratic equations. It was spur of the moment, but it’s been nagging in my head that I should really write down (in)formally some reason why we care about roots.

“Roots” is actually just one name. It’s a cute term that works with the analogy for this essay. But, you may be more familiar with “zeros” or “solutions”. Let’s start with a simple function:
When we ask for the roots of this function, we are asking the question “what input x makes this function zero?” More mathematically, we are asking to solve the equation:
So, roots are the inputs that make a function equal to zero. But, why is that important? Why do we care when something equals zero?
Before I give my answer and philosophy for it, this is supposed to be an exploration of new math ideas for me. So, walk with me through the different “root-finding” methods smarter people have come up with. To practice my video lecture skills, I opted to include video explanations for this section! This will be the first public video lesson!!
I need to make some assumptions about the function f(x) we're dealing with. A function is continuous if you can take a pen and draw the graph of the function without ever lifting your pen. This gives us something very special, the Intermediate Value Theorem, which states
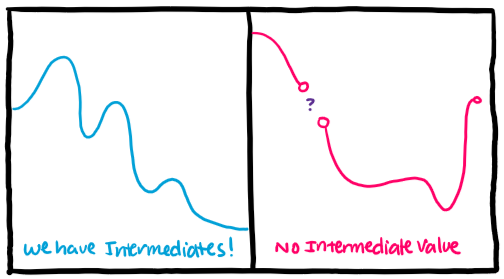
In less math-y terms, if your function is continuous, then it cannot skip a number between the outputs. There is always an input value for every output value between the region! This is extremely useful. In our case, if our function is positive on one end and negative on the other, then that means zero is in the output and so there's a c between a and b such that f(c) = 0.
To make things interesting, we'll assume on the left end, we're positive, and on the right end, we're negative! Alright, let's tackle two methods.
Bisection Method
Newton's Method
These two methods are two starting points for two techniques in root-finding. Bisection method uses the region of inputs to shrink down to a neighborhood around the root. Newton’s method uses tangent lines and calculus to find the root. There are other methods, with much more complexity and accuracy than these. You can breeze through some of them in the root-finding algorithms Wikipedia page.
Let’s go back to why. Why do we care about zeros of a function?
As an easy example, suppose the money in our bank account is represented by the function M(t) where t is the input of time. Knowing when our bank account will become zero would help us plan for the future.
For those who’ve had Calculus or in Calculus right now, you’ll know that whenever the derivative of a function is zero, then we could be at a maximum or minimum of the original function.
As a silly calculus-driven example, suppose you’re selling t-shirts at an event and based on research, you know that your profit follows the function P(s) where s is the input of how many shirts you sell. You know that if you sell too much, you’re going to sour the crowd and lose out on money. So, how do you know when you should stop selling t-shirts to maximize profits? With the help of derivatives, you can find where the roots of the derivatives are and find out where maximum profit could occur.
The existence and relevance of zero is a key development in mathematics, because turns out “nothing” is actually important!
Another important aspect of roots is factorization, but I think I’ll only tease that topic here. To give myself something to talk about in the future, haha.
We have barely scratched the surface! We’ve only been dealing in the two-dimensional world. Imagine what kind of applications we could have if we’re allowed in higher dimensions. Finding roots for a higher dimension is like asking where the peak of the mountain is!
For a relatively simple example, suppose you’re selling two different things. Your profit is a function that depends on two inputs, the amount of x items you sell and the amount of y items you sell. If you want the maximum of this function, you’re going to need to know where the roots of its derivative are. The roots of the derivative could be where the peaks of this mountain are.
Thank you for reading this essay. I hope you’ve found a new appreciation to why we like zeros and roots.

Uploaded 2022 January 15. This is a part of a monthly project which you can read about here.